Describe the Symmetry of These Functions.

By Da_Janae70 09 May, 2022 Post a Comment

Function negation removes half of the entities under the rule. F is an even function.

Graphs Of Quadratic Functions Match Mine Kagan Quadratics Quadratic Functions Vocabulary Words

Which expression is equivalent to 33 22.

. The graphs of certain functions have symmetry properties that help us understand the function and the shape of its graph. Use the graph to complete the table of values. The imaginary line or axis along which you can fold a figure to obtain the symmetrical halves is called the line of symmetry.

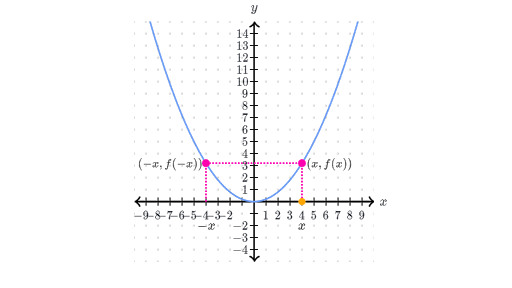
It means one-half is the mirror image of the other half. One can call these the odd functions. Fx is evenit is symmetrical with respect to the y-axisbecause fx fx.

If odd the function is symmetric about the origin. These images are depicting one most important property of reflection symmetry - The first image on the left follows lateral inversion that is left side appears to be the right side as it happens when you look in a mirror. Describe the symmetry of these functions.

Using symmetries these 16 functional varieties reduce to four abstract forms. Because of your favorite lemonade it is 384 for 3 gallons. Write this as an unit rate.

This graph shows a. There are only two symmetries. Any odd function f f f must satisfy f x f x.

Then we see that considered as functions from the face to itself f f e. F x 5x3 f x 5 x 3. Describe the symmetry of these functions.

Complete the following sentences. A function is even if it is symmetric with respect to reflection about the y y y-axis. Functions can be symmetrical about the y-axis which means that if we reflect their graph about the y-axis we will get the same graph.

The function f shown in the graph is an even function. Next there is origin symmetry or rotational symmetry. There are other functions that we can reflect about both the x- and y-axis and get the same graph.

This graph shows a portion of an even function. If an object is symmetrical it means that it. In geometry symmetry is defined as a balanced and proportionate similarity that is found in two halves of an object.

We discuss symmetry about the x-axis y-axis and the origin and we give methods for determining what if any symmetry a graph will have without having to actually graph the function. You can include functions like y x y x3 y sin x and y 1 x. This graph shows a portion of an odd function.

A polynomial will be an even function when all the exponents are even. Given F add F. F is over the interval 2 x 5.

F x x5 - 3x3 2 x f x 1 x. What is its circumference its circumference. The identity and the left-to-right flip reflection over the vertical axis.

Describe the symmetry of these functions. Mathematics 21062019 1300 vlactawhalm29. 1 1 3 3.

The red arrows describe the flip over the vertical axis. Line only rotational only even neither odd. Mathematics 21062019 1430 libby143.

Describe the symmetry of these functions. Negation of the entire function. 1 Show answers Another question on Mathematics.

For example consider the function f x x4 2x2 3 f x x 4 2 x 2 3 shown in Figure 13 a. A Rotation b Reflection. Describe the symmetry of these functions.

Thats not unusual as most functions dont have any of these symmetries. This generates either of the single columns directly above. Use the graph to complete the table of values-2-1-2-3.

Mathematics 20062019 1804. Negation of each variable. Line only rotational only even neither oddDetermine whether eachfunction is even odd or neither.

If it was line symmetry it would need to. Suppose the radius of a circle is 16. 1 Show answers Another question on Mathematics.

Remmi wrote the equation of the line y⅓x2 he solved for x and got x3y-2 which of the following is an equivalent equation for x. The graph has been hidden for x 0. F x f x.

Describe the symmetry of these functions two different answers plz answer asap Other questions on the subject. These are two types of symmetry we call even and odd functions. The line symmetry only has the characteristic of having two equal figures that appear if you put a divisive line in the middle and both parts of the function mirror themselves with the other rotational symmetry means that if you rotate the function 180º you get the same function with the same shape and measures.

If we take the part of the curve that lies to the right of the y y -axis and flip it over the y y -axis it lays exactly on top of the curve to the left of the y y -axis. Some other even functions include y 1 x2 y cos x and y x4 and similar transformations where the new function is not removed from its position at the y-axis. Determine if the function is odd even or neither in order to find the symmetry.

And odd if it is symmetric with respect to 18 0 180circ 1 8 0 rotation. Call the identity e and the flip f. E x2 y2 1 Show Solution.

Neither Dimetri says that a function that is made of terms where the variable is raised only to an odd power will be an odd function. A polynomial will be an odd function when all the exponents are odd. Look at the shape on the left side and identify how the shape has been transformed.

Check x-axis symmetry first. Describe the symmetry of these functions. What issuppose the radius of a circle is 16.

Any even function f f f must satisfy f x f x. F is over the interval 0 x 2. Other questions on the subject.

Created by Sal Khan.

Symmetries Of A Graph Maple Help

Function Symmetry Introduction Article Khan Academy